Почта в Находке
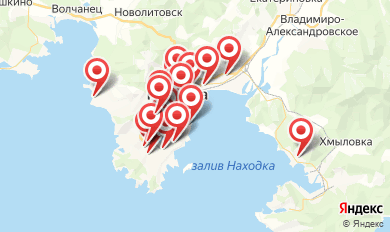
- ↪ Почта – мы нашли для вас 👉 24 организации в Находке;
- ↪ В каждой анкете есть прямой телефон, точный адрес и цены на услуги;
- ↪ Почта в Находке – отзывы оставили посетители
24 организации и 0 отзывов. Средний рейтинг по отзывам 🌟4.3
Очистить всё